你所进行的A/B测试可能存在误区

在A/B实验不断走红的今天，越来越多的企业开始意识到A/B实验的重要意义，并试图通过A/B实验，前置性地量化决策收益，从而实现增长。然而，当你和其他业务伙伴谈及A/B实验时，你总能听到这样的论调：

“这事儿很简单，做个实验就行了。准备两个版本，在不同渠道里发版，然后看看数据。”

“把用户按照did（device_id)尾号奇偶分流进实验组和对照组，然后看看数据表现。”

不可否认，这部分企业的确走在前沿，初步拥有了A/B实验的思维。然而令人遗憾的是，他们操作的所谓“A/B实验”，其实并不具备A/B实验应有的功效。

更令人遗憾的是，他们似乎对此并不知晓。

对于A/B实验原理认知的缺失，致使许多企业在业务增长的道路上始终在操作一批“错误的A/B实验”。这些实验并不能指导产品的优化和迭代，甚至有可能与我们的初衷背道而驰，导致“负增长”。

因此，为了能够更好地明白什么是A/B实验，我们不妨先来了解几种错误的A/B实验。

No1：用户抽样不科学

丨 典型表现

“用户抽样不科学”是错误A/B实验的第一宗罪。操作这种错误A/B实验的企业常采取以下做法：

• 实验中，在不同的渠道/应用市场中，发布不同版本的APP/页面，并把用户数据进行对比；
• 简单地从总体流量中抽取n%用于实验，不考虑流量分布，不做分流处理（例如：简单地从总体流量中任意取出n%，按照ID尾号单双号把用户分成两组）。

丨错在哪儿

不同应用市场/渠道的用户常常带有自己的典型特征，用户分布具有明显区别。对总流量进行“简单粗暴”地抽样也有着同样的问题——分流到实验组和对照组的流量可能存在很大的分布差异。

实际上，A/B实验要求我们，尽可能地保持实验组和对照组流量分布一致（与总体流量也需保持分布一致），否则得出的实验数据并不具有可信性。

为什么要保持分布一致呢？我们不妨来看一个问题。

某大学由两个学院组成。1号学院的男生录取率是75%，女生录取率49%，男生录取率高于女生；2号学院男生录取率10%，女生录取率5%，男生录取率同样高于女生。问：综合两个学院来看，这所大学的总体录取率是否男生高于女生？

直觉上来说，许多人会觉得，男生录取率总体上会高于女生。然而事实并不是这样，让我们来看看实际数字：

从上表可以看出，尽管两个学院男生录取率都高于女生，但综合考虑两个学院的情况时，男生的总体录取率却要低于女生。这种现象在统计学中被称为辛普森悖论。

辛普森悖论由英国统计学家E.H辛普森于1951年提出。其主要内容是：几组不同的数据中均存在一种趋势，但当这些数据组合在一起后，这种趋势消失或反转。其产生的原因主要是数据中存在多个变量。这些变量通常难以识别，被称为“潜伏变量”。潜伏变量可能是由于采样错误造成的。

在A/B实验中，如果实验组和对照组的样本流量分布不一致，就可能产生辛普森悖论，得到不可靠的实验结果。

分流是A/B实验成功与否的关键点，在早期企业还不具备过硬研发能力情况下，想要真正做对A/B实验，最佳方法是借助第三方实验工具中成熟的分流服务。

在前一篇《火山引擎A/B测试》中，我们曾提到火山引擎A/B测试长期服务于抖音、今日头条等头部互联网产品，分流服务科学可靠，并且能够支撑亿级DAU产品进行Push实验，在高并发场景下保持稳定，帮助我们从总体流量中更加均匀地分流样本，使实验更科学。

No2：互斥层选择错误

丨典型表现

接入了实验工具，A/B实验就能做对了吗？也不尽然。许多实验者在进行实验操作时，将有关联性的实验放置在不同的实验互斥层上，导致实验结果不可信。

何谓“互斥层”？在火山引擎A/B测试中，“互斥层”技术是为了让多个实验能够并行，不相互干扰，且都获得足够的流量而研发的流量分层技术。

假设我现在有4个实验要进行，每一个实验要取用30%的流量才能够得出可信的实验结果。此时为了同时运行这4个实验就需要4*30%=120%的流量，这意味着100%的流量不够同时分配给这4个实验。那么此时我只能选择给实验排序，让几个实验先后完成。但这会造成实验效率低下。试想一下，抖音每天有上千个实验要进行，如果只能排队挨号，抖音的实验schedule恐怕要排个10年。

那么有没有办法可以解决这个问题呢？

有，就是使用互斥层技术，把总体流量“复制”无数遍，形成无数个互斥层，让总体流量可以被无数次复用，从而提高实验效率。

各互斥层之间的流量是正交的，你可以简单理解为：在互斥层选择正确的前提下，流量经过科学的分配，可保证各实验的结果不会受到其他互斥层的干扰。

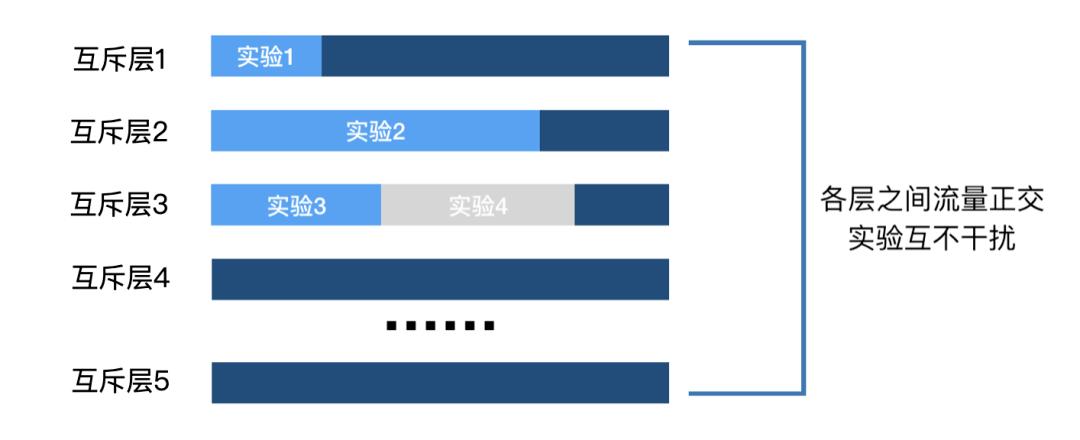
在选择互斥层的时候，实验者应当要遵循的规则是：假如实验之间有相关性，那么实验必须置于同一互斥层；假如实验之间没有相关性，那么实验可以置于不同互斥层。如果不遵循这一原则，那么A/B实验就会出问题。

丨错在哪儿

那么，问题究竟是出在了哪儿呢？

对于实验需求旺盛的企业来说，互斥层技术完美解决了多个实验并行时流量不够用的问题。然而，乱选互斥层会导致实验结果不可信。为什么？举个例子，现在我们想对购买页面的购买按钮进行实验。我们作出两个假设：

• 假设1：将购买按钮的颜色从蓝色改为红色，用户购买率可以提高3%；
• 假设2：将购买按钮的形状从方形改为圆形，用户购买率可以提高1.5%。

针对上述两个假设，我们需要开设两个实验：一个针对按钮颜色，一个针对按钮形状。两个实验均与购买按钮有关系，具有明显的关联性。这两组实验是否可以放在不同互斥层上呢？

丨情况1：相关实验置于不同层#

如下图，我们把两个实验分别放置在两层上，同时开启两个实验。

此时用户A打开了我们的购买页面，进入到总体流量之中。在互斥层1里，用户被测试按钮颜色的实验命中，进入实验组Red；在互斥层2里，用户被测试按钮形状的实验命中，进入实验组Round。

由图可知，用户A将受到“按钮颜色Red”以及“按钮形状Round”两个策略影响，我们无法判断究竟是哪个策略影响了该用户的行为。换句话说，由于两个实验存在关联，用户重复被实验命中，实验结果实际受到了多个策略的影响。这种情况下，两个实验的结果便不再可信了。

丨情况2:相关实验置于同一层

换个思路，如果将上面的两个实验放置在同一层上，那么用户在进入实验后便只会被一个实验命中。两个实验组均只受到一个策略影响，实验结果可信。

企业在进行A/B实验时，工具是基础设施，在实际业务，我们还需要结合具体的实验场景，进行正确的实验设计。

No3：不考虑是否显著

丨典型表现#

实验结束后，只简单地观测实验数据的涨跌，不考虑实验结果是否显著。

丨错在哪儿

“显著”是一个统计学用词，为什么我们需要在评估实验结果时引入统计学呢？

我们已经知道，A/B实验是一种小流量实验，我们需要从总体流量中抽取一定量的样本来验证新策略是否有效。然而抽样过程中，样本并不能完全代表整体，虽然我们竭尽全力地进行随机抽样，但最终仍无法避免样本和总体之间的差异。

了解了这一前提我们就能明白，在A/B实验中，如果只对数据进行简单的计算，我们对于实验结果的判断很可能会“出错”（毕竟我们通过实验观测得到的是样本数据，而不是整体数据）。

那么，有什么办法去量化样本与总体之间的差异对数据指标造成的影响呢？这就需要结合统计学的方法，在评估实验结果时加入相应的统计学指标，如置信度、置信区间、统计功效等。

原则上，如果实验结果不显著（或说不置信），我们便不能判断数据的涨/跌，是否是由实验中采取的策略造成的（可能由抽样误差造成），我们也不能盲目地全量发布新策略/否定新策略。

A/B实验中的统计学原理是一个较为庞大复杂的课题，介于篇幅，我们在此暂不做展开解释。对这部分内容感兴趣的读者也可关注本公众号，我们在后期会推出相应内容来为大家进行讲解。需要明确的一点是：评估A/B实验，绝不仅仅是比较下实验组和对照组的数据高低这么简单。

在实验结果评估方面，好的实验平台需要具备两个特点：第一是可靠的统计策略，第二是清晰、完善的实验报告。相较于市面上其他实验工具，这两个特点正是火山引擎A/B测试的优势所在。

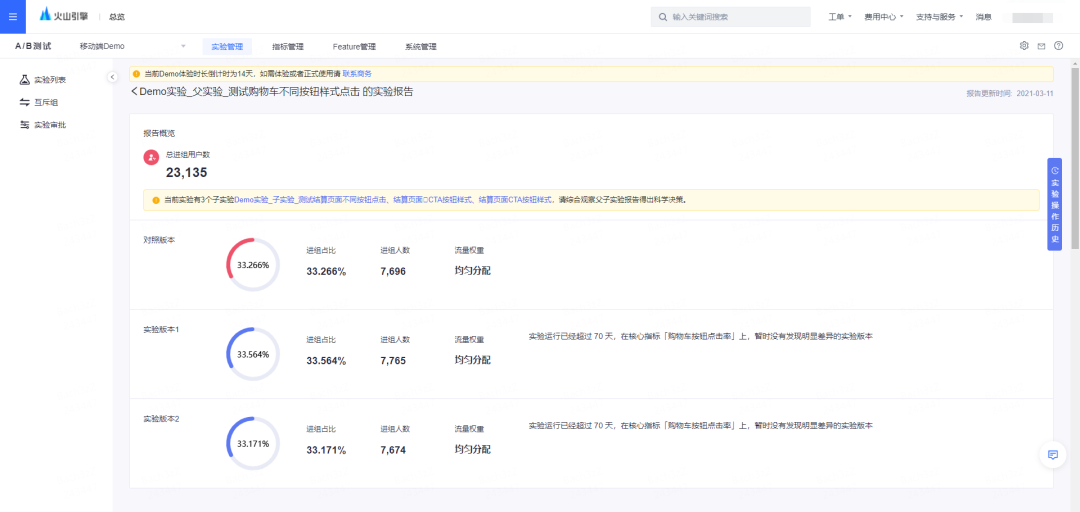
在统计策略方面，火山引擎A/B测试的统计策略长期服务于抖音、今日头条等产品，历经打磨，科学可靠；在实验报告方面，从概览至指标详情，火山引擎A/B测试依托于经典统计学的假设检验方法，结合置信度、置信区间，帮助实验者全方位的判断实验策略收益。

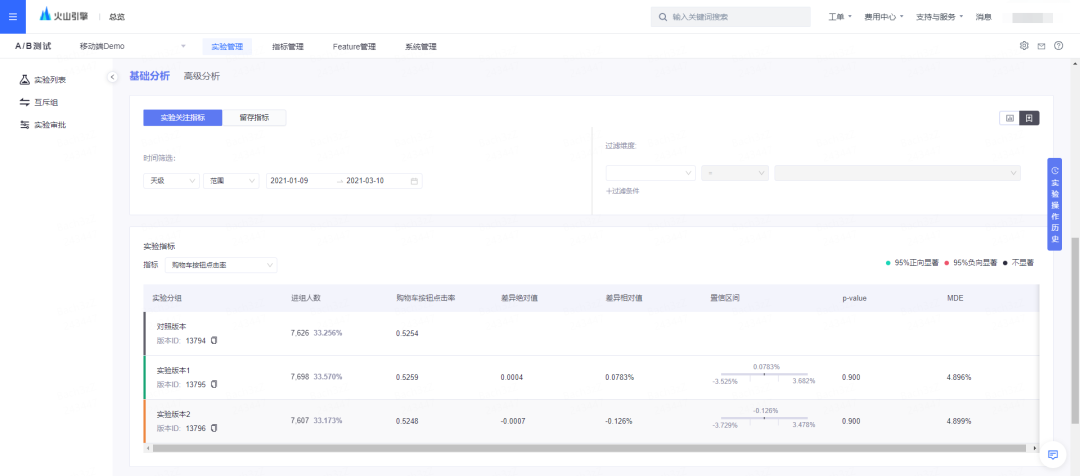
作为互联网公司的新宠，A/B实验确有其独到之处，但浅显的实验认知、错误的实验方法，可能会致使企业在增长的道路上“反向前行”。此处让我们借用一句经典的影视台词吧：“发生这种事，大家都不想的。”

原文链接：https://www.volcengine.com/docs/6360/68691